Vol.2 [수학자의 연구 노트] 내 수학 인생을 바꾼 단 하나의 연구

• 기초과학연구원(IBS)은 세계 수준의 기초과학 연구를 위해 2011년 대한민국이 설립한 연구기관입니다. 수학 분야에서는 5명의 연구책임자가 이끄는 3개의 연구단이 활발한 연구를 펼치고 있습니다. IBS는 설립 10주년을 맞아 <수학동아>와 함께 IBS 수학자들의 연구와 삶을 소개하는 시리즈 <나의 삶, 나의 수학>을 연재합니다. 첫 번째로 점과 선으로 그래프를 그리듯 전 세계 많은 수학자와 교류하며 엄상일 CI(Chief Investigator)가 그린 수학 인생 그래프를 살펴봤습니다.

제가 하던 수학 연구는 길게는 수년, 짧게는 수일 만에 완성되기도 했습니다. 그중 독일의 한 소도시에서 했던 연구는 단 하루 만에 답을 얻었습니다. 그래프 알고리듬 분야에서 유명한 브루노 쿠르셀 프랑스 보르도컴퓨터과학연구소(LaBRI) 교수님과 만났던 2004년 5월에 생긴 일입니다.

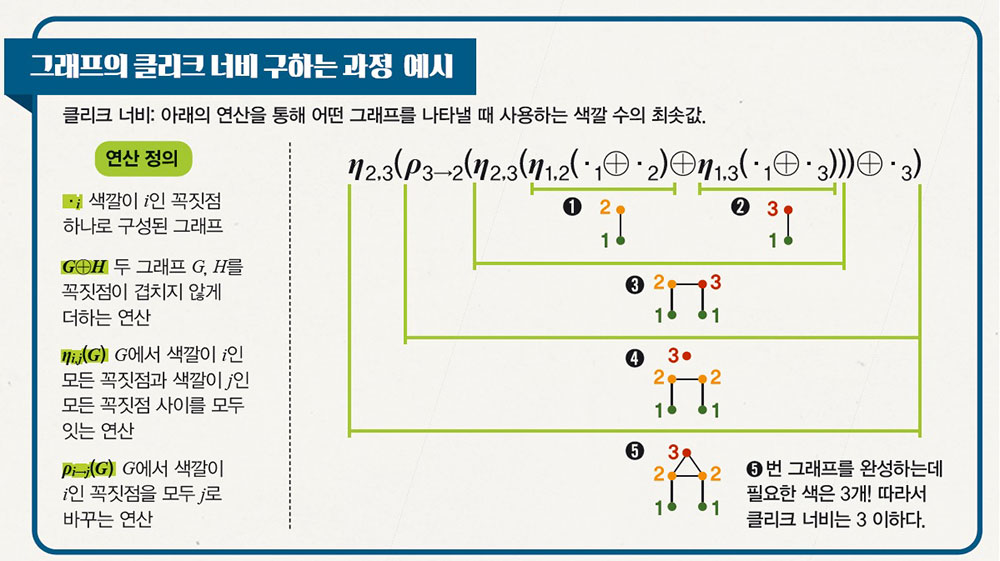
2004년 5월 25일 화요일, 아침 식사를 하는데 쿠르셀 교수님이 오시더니 수십 장의 A4 용지에 손으로 적은 증명을 보여주며 말했습니다. “어제 너와 논의한 내용을 다 썼으니 이따 쉬는 시간에 함께 검토해보자”라고요. 그날 전까지 무슨 일이 있었던 것일까요?

박사 학위를 향한 마지막 한 문제

2002년 가을, 미국 프린스턴대학교 대학원에서 2년차가 됐을 때 입니다. 그래프 이론과 알고리듬을 모두 좋아하는 제 성향을 파악한 지도교수 폴 시모어 미국 프린스턴대 수학과 교수님은 박사학위 주제로 그래프의 ‘클리크 너비(Clique-width)’가 k 이하인지 다항식 시간 안에 판별하는 알고리듬을 만들어보는 문제를 제안해 주셨습니다.

클리크 너비는 1993년 쿠르셀 교수님이 다른 두 교수님과 쓴 논문에서 처음 소개된 개념으로, 그래프가 트리 구조로 얼마나 잘 분해되는지 그 정도를 보여주는 값입니다. 이 개념으로 그래프가 얼마나 복잡한지를 알 수 있죠.

쿠르셀 교수님은 2000년 쿠르셀 정리를 클리크 너비에 대해 확장한 것으로 유명합니다. 어떤 문제를 ‘단항 이차 논리’라는 논리식으로 표현할 수 있을 때, 클리크 너비가 작은 그래프에서 적은 수의 색만 써서 오른쪽의 연산으로 그 그래프를 표현할 방법이 있다면 문제가 참인지를 빠르게 판별할 수 있는 알고리듬을 만들 수 있다는 내용입니다.

하지만 쿠르셀 정리의 전제가 되는 클리크 너비가 비교적 작은 그래프에서 그 그래프를 적은 수의 색깔만 써서 연산으로 표현하는 방법을 찾는 데 문제가 있었습니다. 짧은 다항식 시간 안에 그걸 하는 알고리듬이 없었기 때문이죠. 그래서 박사과정을 밟는 동안, 이 알고리듬이 가능할지 알아보고 가능하다면 직접 이 알고리듬을 만들기로 했습니다. 곧 지도 교수님과 함께 클리크 너비와 똑같은 성질을 가지면서도 더 간단하게 그래프의 복잡도를 나타낼 수 있는 ‘랭크 너비(Rank-width)’라는 개념을 생각해냈습니다. 이를 이용해 클리크 너비 범위에 대한 문제를 랭크 너비에 대한 문제로 바꿔 풀 수 있었습니다.

우연히 가게 된 독일 닥스툴 워크숍

쿠르셀 교수님을 직접 뵐 기회가 생긴 건 2004년입니다. 그래프 이론 분야의 또 다른 수학자인 안드레아스 브란츠테트 독일 로스토크대학교 교수님의 개인 홈페이지를 보다가 2004년 5월 23일부터 1주일간 독일 닥스툴에서 워크숍이 열린다는 걸 알게 됐거든요. 하지만 초청받은 사람만 워크숍에 참석할 수 있었기 때문에 다짜고짜 브란츠테트 교수님께 이메일로 초청해줄 수 있는지 물었는데 다행히 초청장을 받을 수 있었습니다.

이 시기에는 여러 가지로 운이 좋았습니다. 지도교수님도 “이제 포기하고 다른 문제를 해보면 어떠냐”고 권할 정도로 한참 동안 연구에 진척이 없다가 갑자기 그해 봄부터 큰 진전이 생겼거든요.

그래프의 랭크 너비가 엉뚱하게 조합론의 매트로이드(Matroid) 이론과 연결된다는 걸 알게 된 이후부터였습니다. 매트로이드 이론은 행렬의 성질과 그래프의 성질을 통합해서 연구할 수 있는 대상이에요. 이를 연구한 논문에 적힌 연구 방법들을 검토하다 보니 당장 풀어야 할 문제와는 거리가 멀어 보이지만, 랭크 너비에서도 재미있는 결과를 증명할 수 있었습니다.

그중 하나가 1991년에 제기된 제제의 추측과 관련된 내용입니다. 당시 쿠르셀 교수님이 홈페이지에 공개한 최신 논문 중에 독일 수학자 데틀레프 제제의 추측에 관한 논문이 있었습니다. 제제의 추측은 ∧, ∨, ∈, ∀, ∃ 같은 기호를 써서 ‘단항 이차 논리’로 표현된 논리식이 어떤 그래프 집합에서 항상 참인지 아닌지 판별해주는 알고리듬이 존재하려면, 그 그래프 집합의 클리크 너비가 무한히 커질 수는 없다는 것이었습니다. 문제를 나타내는 논리식의 표현력이 약하면 알고리듬이 쉽게 참인지 판별할 수 있겠지만, 표현력이 강하면 너무 많은 조건을 표현할 수 있게 돼 판별하지 못하는 문제도 표현할 수 있게 됩니다. 제제의 추측은 단항 이차 논리로 문제의 범위를 제한하면, 절묘하게도 클리크 너비가 작을 때는 답을 할 수 있고 클 때는 답을 할 수 없는 경계가 생긴다는 추측입니다.

쿠르셀 교수님은 그래프 꼭짓점 집합을 두 부류로 잘 나눠 한 부류에서 다른 부류로 가는 선만 있는 경우라면 제제의 추측이 해결된다는 것을 증명했습니다. 마침 진행하던 연구에서 그런 그래프에서는 랭크 너비를 매트로이드 이론과 연관 지을 수 있다는 것을 알게 됐습니다. 그리고서 불과 며칠 후에 워크숍에서 쿠르셀 교수님을 만나 이야기할 수 있게 됐습니다.

▲ 2004년 닥스툴 워크숍 단체 사진. 필자는 가장 뒷줄, 쿠르셀 교수 님 바로 뒤에서 웃고 있다.

쿠르셀 교수와의 공동 연구

닥스툴에서 열린 워크숍은 공동 연구를 하기 좋은 방식으로 이뤄졌습니다. 오전에는 최신 연구결과를 듣고 오후에는 삼삼오오 모여서 함께 연구했죠. 워크숍 첫날 오전에는 강연이 있었고 오후가 돼서야 쿠르셀 교수님과 논의를 할 수 있었습니다. 쿠르셀 교수님에게 랭크 너비와 매트로이드 이론을 연결해 어떤 결과를 증명했는지 설명하고, 그것으로 제제의 추측을 얼마나 증명할 수 있을지 한참 논의했습니다.

곧 제제의 추측에서 문제를 표현하는 논리식에 어떤 집합의 원소 개수가 홀수인지 짝수인지를 묻는 것을 허용해 표현력을 조금 더 강하게 만들면, 제제의 추측이 참임을 증명할 수 있었습니다. 즉 단항 이차 논리식에 집합의 크기가 홀수인지 짝수인지 판별하는 것까지 포함하고 이런 식으로 표현 가능한 문제가 주어질 때 어떤 그래프집합에서 그 논리식이 항상 참이 되는지 대답할 수 있다면 그 그래프 집합은 랭크 너비, 클리크 너비가 작다는 것을 증명한 거죠. 게다가 그래프의 랭크 너비가 k 이하인지 판별하는 다항식 시간 알고리듬까지 얻었습니다. 논의한 지 몇 시간 만에 제제의 추측을 살짝 약하게 만든 것을 증명했을 뿐 아니라 박사과정의 연구 주제까지 해결했던 것이지요. 박사과정 연구 주제와 제제의 추측은 겉으로 보기엔 다르지만, 본질적으로 같았기에, 문제 하나를 풀었더니 다른 하나도 해결할 수 있었던 겁니다.

그래서 예정에 없이 그 워크숍 마지막 날 아침에 쿠르셀 교수님과의 새로운 연구결과를 짧게 발표했습니다. 워크숍 결과보고서에는 최대 연구 성과로 저와 쿠르셀 교수님의 공동 연구가 꼽혔죠. 이후 여름 내내 논문을 완성해 투고했고 2007년 논문이 ‘조합론저널B’에 출판됐습니다. 박사 학위 논문의 4분의 1은 이때의 결과 덕분에 가능했다고 볼 수 있죠. 2010년 받은 대한수학회 논문상도 마찬가지고요.

망설이지 않고 먼 거리를 떠나 다른 나라의 수학자와 했던 소통이 수많은 성과로 나타났던 중요한 경험이었습니다. 코로나19로 다른 수학자와 해외 교류가 쉽지 않은 지금도 온라인으로 만나면서 끊임없이 논의하는 이유입니다.