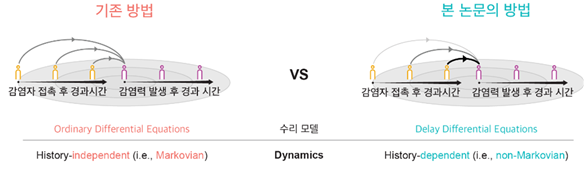
What Was Wrong with Traditional Epidemic Models? — “Models That Forgot the Past”

One of the key indicators describing how fast an infectious disease spreads is the effective reproduction number (R-value), which plays a decisive role in shaping public health policies. However, most widely used epidemic-spread models so far have relied on an unrealistic assumption that all infected individuals transmit the disease with a constant probability.

This assumption corresponds to a Markov process, in which the probability of future infection depends only on the current state, without considering when in the past the infection occurred. In reality, however, the infectiousness of a disease changes over time — for example, an individual’s infectiousness may increase or decrease depending on how much time has passed since infection. This means real-world transmission follows a non-Markovian process more closely. The mismatch can distort estimates of the reproduction number, especially during the early, rapidly changing phase of an outbreak.

Understanding the Reproduction Number

The reproduction number (R) indicates how many additional people one infected person infects on average at a given time, making it essentially the “driving force” of an epidemic. If R exceeds 1, the outbreak grows; if it is below 1, it fades. Because R can show how interventions such as testing, isolation, or vaccination affect transmission early on, it serves as a key policy indicator. However, R is not a simple ratio — it is sensitive to when transmissions occur (the time distribution between infection and secondary transmission). If this distribution is not modeled realistically, R may spike unrealistically high during the initial phase of an epidemic. Therefore, when interpreting R, one must consider realistic generation intervals, as well as policy changes, reporting delays, testing volume, and under-reporting. In short, to make R a reliable compass for public-health decisions, models must capture not only how many transmissions occur but also when they occur.

Estimation Based on a Non-Markovian Infection Model

Transmission evolves over time: right after infection, contagiousness is low; it peaks at a certain time and then gradually declines. The non-Markovian approach incorporates this time dependence directly into the model. Instead of assuming a simple exponential distribution, it uses more realistic distributions for infection and incubation periods (for example, a gamma distribution) to represent when infectiousness rises and how long it lasts. By combining this with Bayesian inference, the model can estimate key epidemiological variables — such as the reproduction number and infectious period — with high accuracy even from case counts alone. This makes it extremely useful for real-time epidemic-control planning.

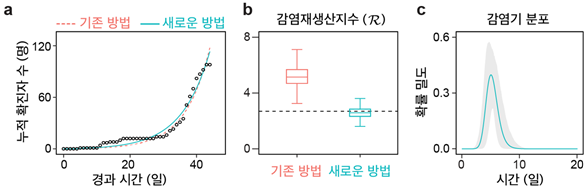
Re-evaluating COVID-19 Data

Applying this method to early-stage COVID-19 data from Korea showed that traditional models (which assume a fixed infectious period) overestimated R at around 4, whereas the new non-Markovian approach yielded R ≈ 2.7 — consistent with actual contact-tracing data. This demonstrates that how a model handles the timing of transmissions can change the interpretation of the same dataset. Moreover, this approach can estimate the infectious-period distribution itself, allowing policymakers to quantitatively assess the impact of interventions such as testing and isolation.

Toward More Refined Policy Decisions

By providing more stable and realistic estimates of R, the new method reflects real changes in the transmission timeline before and after interventions. As a result, it can reduce excessive fluctuations in epidemic-peak forecasts and resource-demand projections. The team’s open-source software package also enables customized simulations that include factors such as vaccination, viral variants, asymptomatic infections, and fatality rates — offering strong potential to improve both the precision and speed of policy design for future emerging infectious diseases.