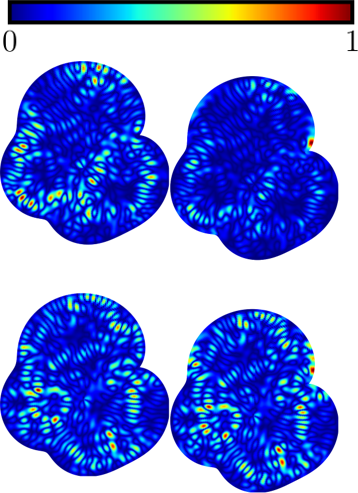
A new study from the Institute for Basic Science (IBS) in South Korea reveals that a widely used method in quantum physics may produce incorrect results when applied to certain high-energy systems. The findings could have significant implications for how physicists model and interpret quantum chaos — the unpredictable behavior of particles in confined systems.

For decades, physicists have used "quantum billiards" as a model to explore how quantum particles behave inside a confined space, much like a billiard ball bouncing inside a table. These systems have been essential in the study of quantum chaos, with applications in areas like nanotechnology, quantum computing, and fundamental physics.

In 1987, a new version of quantum billiards was proposed for relativistic particles — particles moving at speeds close to the speed of light — such as neutrinos. These so-called neutrino billiards follow different rules governed by the Dirac (or Weyl) equation. To simulate such systems, researchers developed various numerical methods, one of which is the conformal-map method (CMM), first applied to this context in a 2013 study published in Physical Review Letters.

However, in the new paper, Dr. Barbara DIETZ and her team at IBS have proven mathematically that the CMM fails when applied to relativistic quantum billiards. Although the method appears to provide plausible results, it actually violates the fundamental equations that govern these systems — and, crucially, it fails to confine particles within the system boundary as required by physical laws.

“This flaw in the method explains long-standing inconsistencies between CMM-generated results and the expected behavior of relativistic quantum systems,” Dr. Dietz explained.
The researchers also demonstrated that even if corrections are applied to the mathematical assumptions of the CMM, the solutions still fail to satisfy the boundary conditions. This undermines several previous studies that used this method to explore so-called quantum scars — patterns of particle behavior that reflect classical trajectories — in relativistic systems.

The work serves as a call for caution in using approximate methods in theoretical physics and emphasizes the importance of rigorous validation, especially when extending classical techniques to relativistic regimes. The study recommends using more reliable alternatives such as the boundary-integral method (BIM), which properly accounts for the mathematical and physical constraints of the system.

Figure 1. The left part shows the outgoing current using the eigenstates computed with BIM, the right one those computed with CMM. For the BIM, the outgoing current vanishes along the boundary as required by the BC, whereas for the CMM, it clearly deviates from zero.