주메뉴
- About IBS 연구원소개
-
Research Centers
연구단소개
- Research Outcomes
- Mathematics
- Physics
- Center for Underground Physics
- Center for Theoretical Physics of the Universe (Particle Theory and Cosmology Group)
- Center for Theoretical Physics of the Universe (Cosmology, Gravity and Astroparticle Physics Group)
- Dark Matter Axion Group
- Center for Artificial Low Dimensional Electronic Systems
- Center for Theoretical Physics of Complex Systems
- Center for Quantum Nanoscience
- Center for Exotic Nuclear Studies
- Center for Van der Waals Quantum Solids
- Center for Relativistic Laser Science
- Chemistry
- Life Sciences
- Earth Science
- Interdisciplinary
- Center for Neuroscience Imaging Research (Neuro Technology Group)
- Center for Neuroscience Imaging Research (Cognitive and Computational Neuroscience Group)
- Center for Algorithmic and Robotized Synthesis
- Center for Genome Engineering
- Center for Nanomedicine
- Center for Biomolecular and Cellular Structure
- Center for 2D Quantum Heterostructures
- Center for Quantum Conversion Research
- Institutes
- Korea Virus Research Institute
- News Center 뉴스 센터
- Career 인재초빙
- Living in Korea IBS School-UST
- IBS School 윤리경영


주메뉴
- About IBS
-
Research Centers
- Research Outcomes
- Mathematics
- Physics
- Center for Underground Physics
- Center for Theoretical Physics of the Universe (Particle Theory and Cosmology Group)
- Center for Theoretical Physics of the Universe (Cosmology, Gravity and Astroparticle Physics Group)
- Dark Matter Axion Group
- Center for Artificial Low Dimensional Electronic Systems
- Center for Theoretical Physics of Complex Systems
- Center for Quantum Nanoscience
- Center for Exotic Nuclear Studies
- Center for Van der Waals Quantum Solids
- Center for Relativistic Laser Science
- Chemistry
- Life Sciences
- Earth Science
- Interdisciplinary
- Center for Neuroscience Imaging Research (Neuro Technology Group)
- Center for Neuroscience Imaging Research (Cognitive and Computational Neuroscience Group)
- Center for Algorithmic and Robotized Synthesis
- Center for Genome Engineering
- Center for Nanomedicine
- Center for Biomolecular and Cellular Structure
- Center for 2D Quantum Heterostructures
- Center for Quantum Conversion Research
- Institutes
- Korea Virus Research Institute
- News Center
- Career
- Living in Korea
- IBS School
News Center
Overcoming Fundamental Limitations of Conventional Infectious Disease Modeling- Joint Research Team from IBS, KAIST, Korea University, and NIMS Develops New Estimation Method Addressing Bias in Infectious Disease Modeling - A recent breakthrough study has introduced a novel methodology that significantly enhances the accuracy of epidemiological estimates for infectious diseases like COVID-19. The study, titled “Overcoming Bias in Estimating Epidemiological Parameters with Realistic History-Dependent Disease Spread Dynamics,” was recently published in Nature Communications. The research team, led by Professor KIM Jae Kyoung at KAIST and Chief Investigator of the Biomedical Mathematics Group within the Institute for Basic Science (IBS), along with Dr. CHOI Sunhwa from the National Institute for Mathematical Sciences (NIMS), and Professor CHOI Boseung from Korea University, addressed a long-standing challenge in infectious disease modeling. Previous models have primarily used history-independent dynamics, which assume a constant probability of transitioning between different disease stages of disease regardless of time since exposure. This approach can lead to significant bias in estimating critical parameters such as the reproduction number (R), latent period, and infectious period. In contrast, the newly developed method by the team adopts a history-dependent framework, where the probability of transitioning between disease stages changes over time. This realistic modeling approach eliminates biases introduced by conventional methods and allows for more accurate predictions of disease spread, even when only confirmed case data are available. This is crucial for determining the effectiveness of intervention strategies like social distancing and vaccination campaigns. Professor KIM Jae Kyoung explained, “Our research represents a paradigm shift in epidemiological parameter estimation. By overcoming the limitations of previous models, we can now provide public health officials with more precise data on disease dynamics. This will enable more effective intervention strategies, ultimately helping us to better manage and control infectious disease outbreaks.” Dr. CHOI Boseung from Korea University, another corresponding author, added, “The new method allows us to estimate the infectious period distribution accurately, even when this period changes over time due to varying intervention measures and disease evolution. This flexibility in parameter estimation was previously impossible using traditional models. Our work will have a significant impact on the way epidemiologists and public health officials respond to future pandemics.” Using early COVID-19 data outbreak from Seoul, South Korea, the team demonstrated that the new method provides much more precise estimates of the reproduction number compared to conventional methods. They found that traditional approaches could overestimate the reproduction number by up to twofold, potentially leading to misguided policy decisions. Dr. CHOI Sunhwa highlighted, “This research marks a significant advancement in our understanding of infectious disease dynamics. The new methodology can provide public health officials with more reliable data, leading to better-informed decisions during pandemics.” The team also developed a user-friendly computational package named IONISE (Inference Of Non-markovIan SEir model), which simplifies the implementation of their advanced inference method. IONISE supports a variety of epidemiological models, making it adaptable to different infectious diseases and intervention scenarios. Dr. HONG Hyukpyo asserts that this methodology will revolutionize the field of infectious disease modeling and epidemiological parameter estimation, paving the way for more effective public health responses and strategies in future pandemics. About the Research TeamThe study was carried out by a collaborative research team from the Department of Mathematical Sciences at KAIST, the Biomedical Mathematics Group at IBS, NIMS, and the Division of Big Data Science at Korea University. With deep expertise in mathematical modeling and epidemiology, the team aims to address critical challenges in infectious disease prediction and control through advanced mathematical frameworks and computational methods. The research was supported by grants from the National Research Foundation of Korea, the Samsung Science and Technology Foundation, and the Institute for Ministry of Education, Basic Science.
Notes for editors
- References
- Media Contact
- About the Institute for Basic Science (IBS)
|
| Next | |
|---|---|
| before |
- Content Manager
- Public Relations Team : Yim Ji Yeob 042-878-8173
- Last Update 2023-11-28 14:20










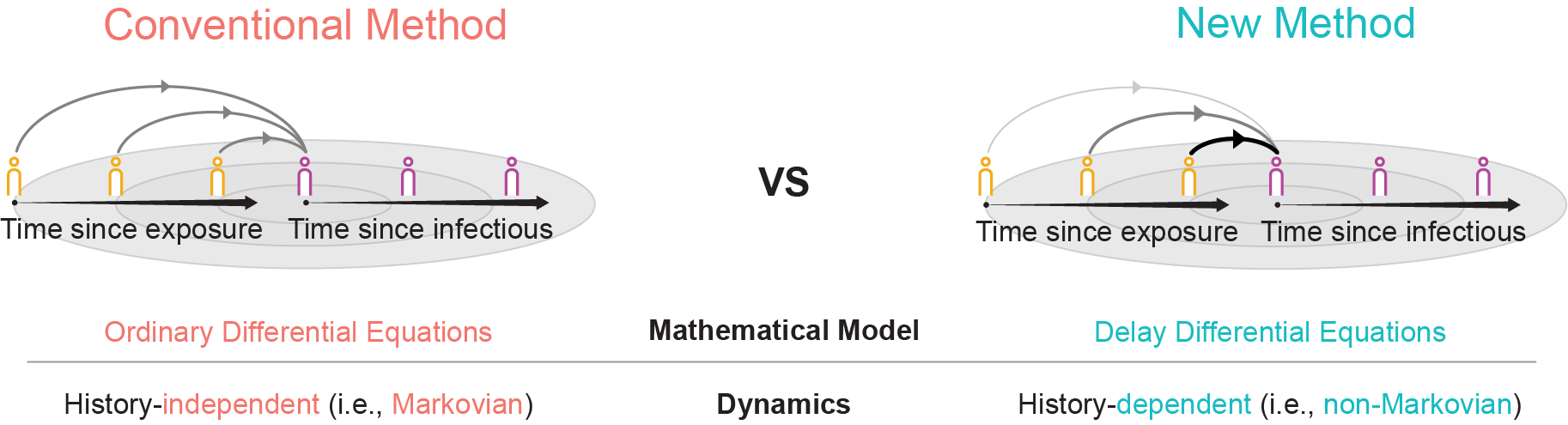 Figure 1. Novel methodology estimating epidemiological parameters based on realistic assumptions
Figure 1. Novel methodology estimating epidemiological parameters based on realistic assumptions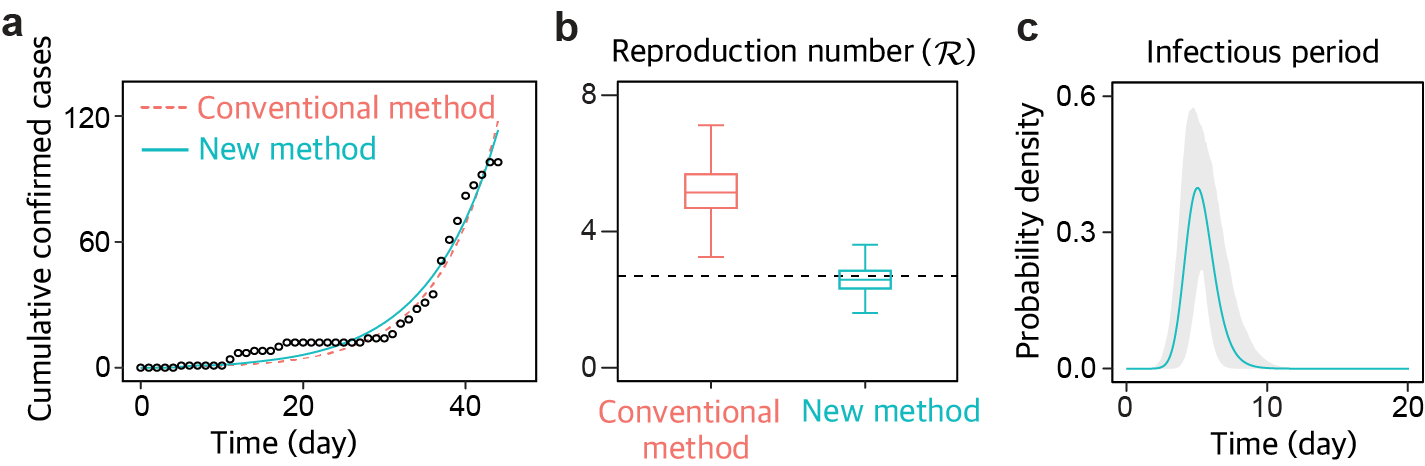 Figure 2. Comparison of estimation results between the conventional and new methods for epidemiological parameters
Figure 2. Comparison of estimation results between the conventional and new methods for epidemiological parameters
