주메뉴
- About IBS 연구원소개
-
Research Centers
연구단소개
- Research Outcomes
- Mathematics
- Physics
- Center for Underground Physics
- Center for Theoretical Physics of the Universe (Particle Theory and Cosmology Group)
- Center for Theoretical Physics of the Universe (Cosmology, Gravity and Astroparticle Physics Group)
- Dark Matter Axion Group
- Center for Artificial Low Dimensional Electronic Systems
- Center for Theoretical Physics of Complex Systems
- Center for Quantum Nanoscience
- Center for Exotic Nuclear Studies
- Center for Van der Waals Quantum Solids
- Center for Relativistic Laser Science
- Chemistry
- Life Sciences
- Earth Science
- Interdisciplinary
- Center for Neuroscience Imaging Research (Neuro Technology Group)
- Center for Neuroscience Imaging Research (Cognitive and Computational Neuroscience Group)
- Center for Algorithmic and Robotized Synthesis
- Center for Genome Engineering
- Center for Nanomedicine
- Center for Biomolecular and Cellular Structure
- Center for 2D Quantum Heterostructures
- Center for Quantum Conversion Research
- Institutes
- Korea Virus Research Institute
- News Center 뉴스 센터
- Career 인재초빙
- Living in Korea IBS School-UST
- IBS School 윤리경영


주메뉴
- About IBS
-
Research Centers
- Research Outcomes
- Mathematics
- Physics
- Center for Underground Physics
- Center for Theoretical Physics of the Universe (Particle Theory and Cosmology Group)
- Center for Theoretical Physics of the Universe (Cosmology, Gravity and Astroparticle Physics Group)
- Dark Matter Axion Group
- Center for Artificial Low Dimensional Electronic Systems
- Center for Theoretical Physics of Complex Systems
- Center for Quantum Nanoscience
- Center for Exotic Nuclear Studies
- Center for Van der Waals Quantum Solids
- Center for Relativistic Laser Science
- Chemistry
- Life Sciences
- Earth Science
- Interdisciplinary
- Center for Neuroscience Imaging Research (Neuro Technology Group)
- Center for Neuroscience Imaging Research (Cognitive and Computational Neuroscience Group)
- Center for Algorithmic and Robotized Synthesis
- Center for Genome Engineering
- Center for Nanomedicine
- Center for Biomolecular and Cellular Structure
- Center for 2D Quantum Heterostructures
- Center for Quantum Conversion Research
- Institutes
- Korea Virus Research Institute
- News Center
- Career
- Living in Korea
- IBS School
News Center
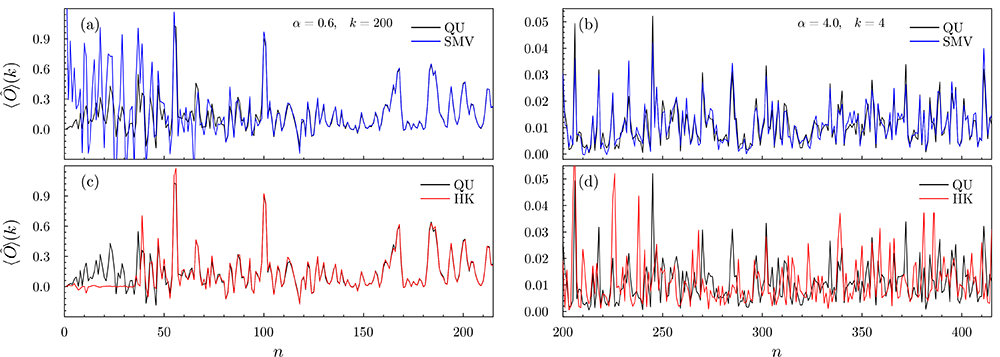
A promising future for novel semiclassical techniques in computational physics- New method for computing quantum mean values bypasses the curse of dimensionality and is more accurate than previously thought possible - Quantum mechanics is a very old theory, having arrived at its modern version almost one hundred years ago. Interestingly, it is significantly older than the classical concept of chaos, which was only established in the 1950s. The discovery of chaotic behavior posed a major barrier to earlier efforts attempting to rigorously bridge classical and quantum mechanics. For consistency reasons, the latter should always allow for the emerge of the former as its classical limit is taken. Such limit turned out to be rather nontrivial, requiring the use of sophisticated mathematical concepts, the most important being stationary phase approximations. These approximations give birth to a formalism valid in an intermediate regime in which quantum numbers are not large enough for the system to be considered near classical, but not small enough for it to be considered purely quantum – the semiclassical regime. Semiclassical physics uses stationary phase approximations in order to take classical information as input and to output quantum interference. The formalism has two very important characteristics: Firstly, it allows us to visualize quantum effects as emerging from interfering classical trajectories, providing quantum mechanics with geometry; Secondly, since it models quantum mechanics based on classical trajectories, it does not scale exponentially with the number of degrees of freedom. The first aspect is a philosophical one that has helped physicists devise and interpret a plethora of experiments, and the second is a computational one that basically states that semiclassical methods can bypass the dimensionality curse found in quantum mechanics. For the latter reason such methods have been consistently employed in many fields of science (especially quantum chemistry) for the past 50 years, being able to model systems with dozens of degrees of freedom (which are intrinsically semiclassical due to their sizes). Semiclassical methods, however, suffer from two major problems: They typically diverge when the underlying classical dynamics is strongly chaotic; And, sometimes, the stationary phase approximations fail catastrophically. The computation of mean values, for example, is one such occasion in which an absurd result is obtained if stationary phase approximations are blindly employed. In order to remediate this problem, a previous work by researchers at Universite Paris-Saclay focused on establishing a semiclassical method that could deal with mean values, although the method itself had not yet been put to the test [1]. An IBS researcher at the Center of Theoretical Physics of Complex Systems and collaborators have employed the method to compute mean values in a prototype system lying simultaneously in the deep semiclassical and strongly chaotic regimes, both known to be remarkably problematic [2]. For comparisons, one of the most successful and well-known methods in quantum chemistry was also implemented for the same system. Not only was their semiclassical method extremely accurate, but it was also able to deal with regimes in which the standard method produces nothing but numerical noise. Moreover, a rare glimpse into the inner workings of mean values in quantum mechanics is provided, together with how they connect to the geometry of classical physics. These results show that previous problems seen in semiclassical methods, which are very popular in chemistry, are intrinsic to the methods being used instead of a consequence of a general barrier to semiclassics. As a result, more accurate semiclassical methods can be devised that should be able to reach regimes previously thought impossible. These methods, such as our own, can then be expanded to systems with more degrees of freedom or to deal with the propagation of coherent states, which are situations more closely connected to experiments in both physics and chemistry.
Notes for editors
- References
- Media Contact
- About the Institute for Basic Science (IBS)
|
| Next | |
|---|---|
| before |
- Content Manager
- Public Relations Team : Yim Ji Yeob 042-878-8173
- Last Update 2023-11-28 14:20