Skip to content
- Time: August 1 – 6, Korean time:
I. Expanders: 9:30am-10:50am;
II. Topological combinatorics: 11:00am-12:20pm;
III. Convexity spaces: 2:30pm-3:50pm. - Zoom: 819 0982 4573, PW: 202208
Announcement
- Time change: on August 4th (Thursday), Convexity spaces will be at 11am, Topological combinatorics will be at 2:30pm.
Sparsifiers and expanders
- 8/1: Why Laplacian is useful: applications in image processing, analogue of Laplacian operator on Euclidean space.
- 8/2: Random walks on non-regular graphs, spectral sparsifiers with $O(n\log n)$ edges.
- 8/3: Spectral sparsifiers with $O(n\log n)$ edges, Interlacing polynomials.
- 8/4: Spectral sparsifiers with linear many edges.
- 8/5: Existence of bipartite Ramanujan graphs using 2-covers.
- 8/6: Existence of bipartite Ramanujan graphs by taking union of perfect matchings.
Topological combinatorics
- 8/1: Homotopy, Homology, Nerve theorem, good cover, Topological Helly. Tablet note
- 8/2: Three basic tools in topological combinatorics and their equivalence: Brouwer Fixed-Point Theorem/Sperner’s Lemma/KKM Theorem. Tablet note
- 8/3: Brouwer implies weak Sperner, and applications of KKM theorem:(p,q)-theorem/Line transversal/Colorful KKM theorem. Tablet note
- 8/4: Hall’s theorem for hypergraphs, proof based on Sperner’s lemma to an economically hierarchic triangulation of a simplex. Tablet note
- 8/5: Ryser’s conjecture for tripartite 3-uniform hypergraphs, homology nerve theorem, topological Hall theorem. Tablet note
- 8/6: Homology nerve theorem, Topological Hall theorem (correction), $d$-collapsible/Leray complexes, Topological colorful Helly theorem, Alexander duality theorem. Tablet note
Convexity spaces
- 8/1: Examples of convexity spaces: convex lattices sets, subgroups, subtrees, subcubes, invariants abstracting basic properties of Euclidean convexity space: Radon/Carathéodory/Helly. Tablet note
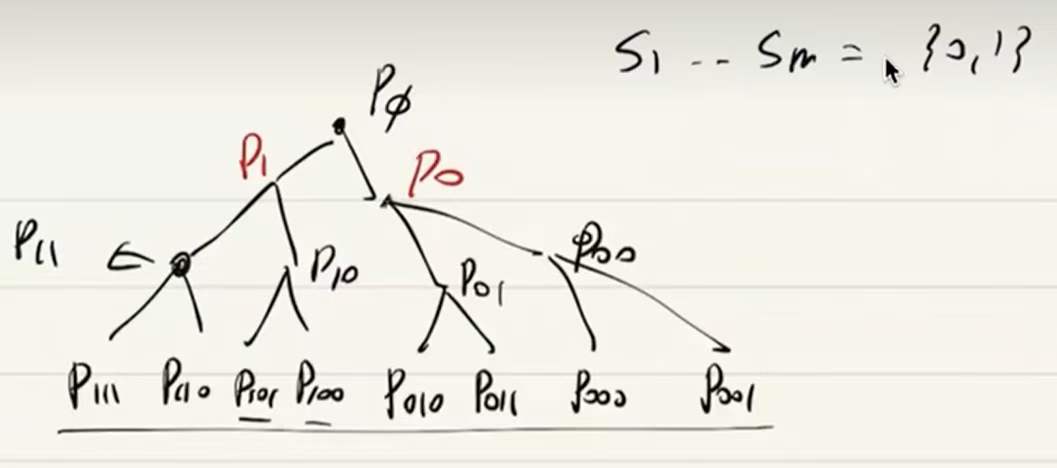
- 8/2: Radon number of subcubes in $\{0,1\}^n$ is about $\log_2 n$, weak $\varepsilon$-net. Tablet note
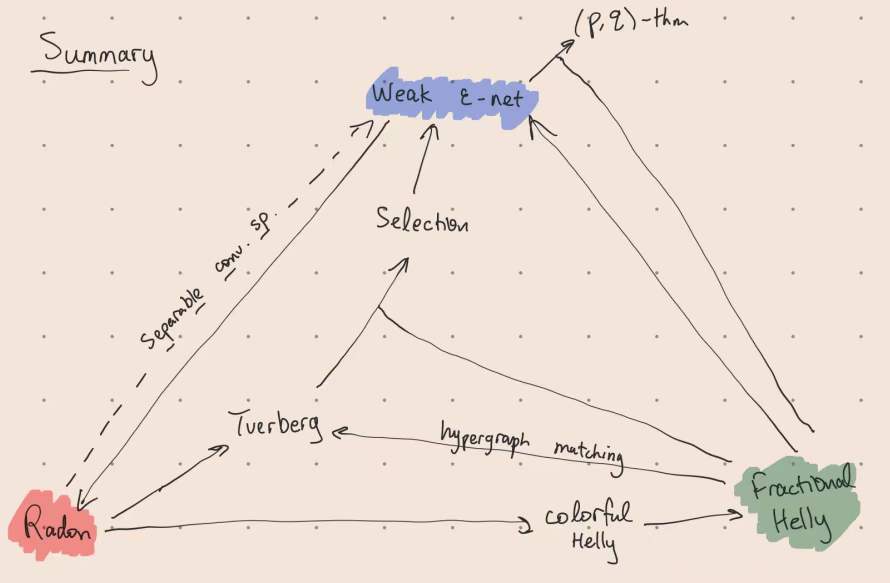
- 8/3: weak $\varepsilon$-net ⇒ Radon, colorful/fractional Helly, Tverberg number. Tablet note
- 8/4: Helly + Tverberg ⇒ colorful Helly ⇒ fractional Helly, Radon ⇒ fractional Helly, selection ⇒ weak $\varepsilon$-net. Tablet note
- 8/5: Fractional Helly ⇒ Tverberg using hypergraph matching, fractional Helly + Tverberg ⇒ selection, equivalent formulation of weak $\varepsilon$-net: bounding transversal number via fractional transversal number. Tablet note
- 8/6: Radon ⇒ weak $\varepsilon$-net in separable convexity space via VC dim. Tablet note